
平行四辺形の面積 S Ad の証明2つ Youtube
平行四辺形を二等分するような直線の式を考えなさい。 というような問題がよく出題されます。 この問題を解くためには、ちょっとした特徴を知っておく必要があります。 それが 対角線が交わる点を通るように 直線をひくと、平行四辺形を二等分できる!長方形の面積 平行四辺形の面積 三角形の面積 台形の面積 円の面積 算数では様々な公式を覚えます。 しかしその公式の意味を知っている方は多くないと思います。 本ホームページでは公式の意味や公式の導き方を図を使用して分かりやすく説明して
平行 四辺 形 計算
平行 四辺 形 計算-向かい合う辺がそれぞれ平行の四角形を『 平行四辺形 ( へいこうしへんけい ) 』と言いますが、平行四辺形の面積は正方形や長方形同様、簡単な計算で求めることができます。 なぜ簡単な計算で求められるのか。それは図形を変形するだけなので、図を使って説明すれば小学生でもすぐに 平行四辺形と長方形の面積は同じになるので、平行四辺形の道の面積も右端に寄せてしまいます。 中の長方形の面積を求めます。 ×30=600㎡ 例3)頂点をまとめて考えます。 *平行四辺形の中の色のついた部分の面積を求めます。
平行四辺形 2辺と間の角度 面積の計算 計算サイト
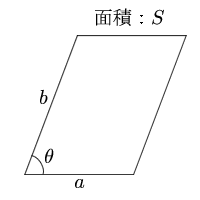
かなり、平行四辺形に近づきました。 この様に細かくしていけばいく程、平行四辺形にどんどん近づいきます。 つまり、円は平行四辺形に変形が可能ということです。 平行四辺形に変形させることができれば、もう計算はできると思います。小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題今回は、 「平行四辺形の面積の求め方」 を学習するよ。 中学校までは、平行四辺形の面積は 「(底辺)×(高さ)」 で求めたよね。 ただし、三角比を知っている僕たちは、 「底辺と、斜めの辺と、はさむ角」 だけが分かっていれば、平行四辺形の面積を求めることができるよ。
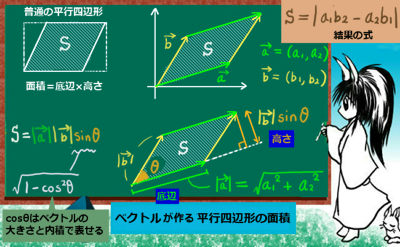
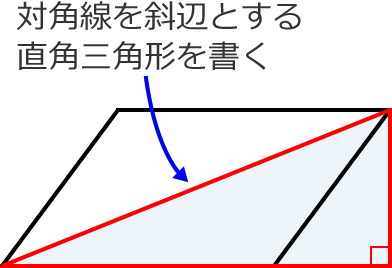
平行四辺形abcdの頂点acから対角線bd上に垂線をひき、対角線との交点をそれぞれefとすれば、四角形aecfは平行四辺形になります。 このことを証明しなさい。 仮定平行四辺形abcd角aef=角cfe=90° 結論? 4の方 法・・対角線がそれぞれの中点で交わる。 ので教えてください!! お願いします! 平方四辺形を対角線で分けた $4$ つの三角形の面積は等しいから、平行四辺形の面積は、 $4\times \dfrac{3\sqrt{3}}{2} = 6\sqrt{3}$ だね! まとめ 平行四辺形の面積を対角線の長さと角度から求めるのに必要な特徴は、5年 平行四辺形の面積|算数イメージ動画集|大日本図書 平行四辺形の面積を求めるにはどうしたらいいでしょうか。 台形を2つ合わせて,あるいは三角形と台形を合わせて長方形にしてみると公式が使えます。 つまり,平行四辺形の面積は 底辺×高さ で
平行 四辺 形 計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 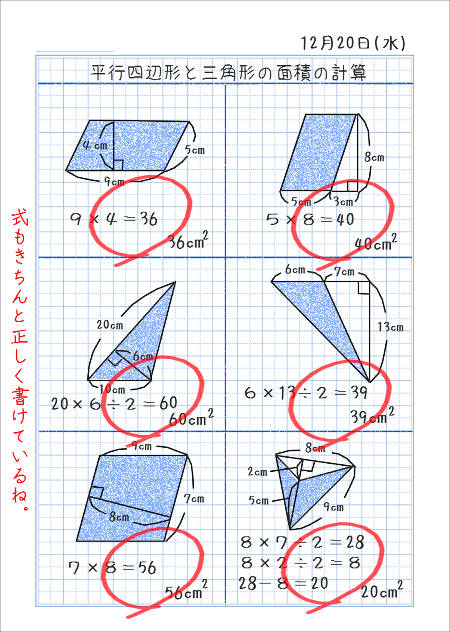 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 | 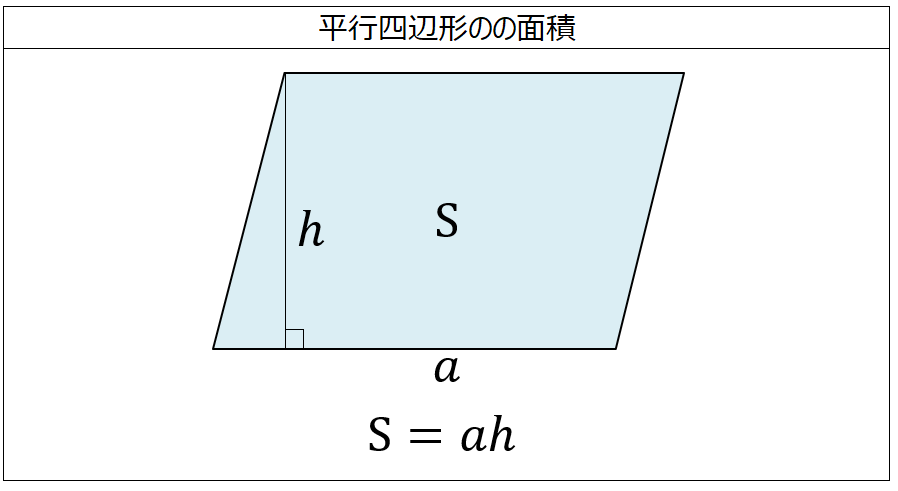 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 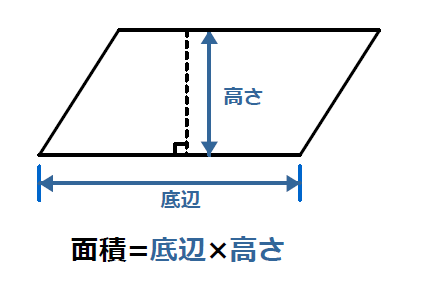 平行四辺形の面積の公式 算数の公式 | 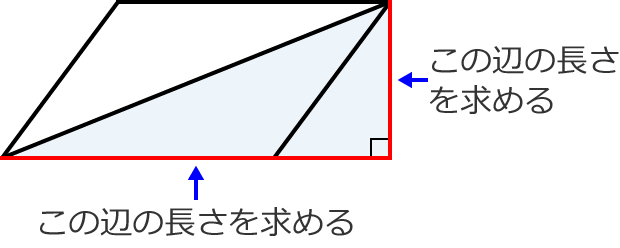 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 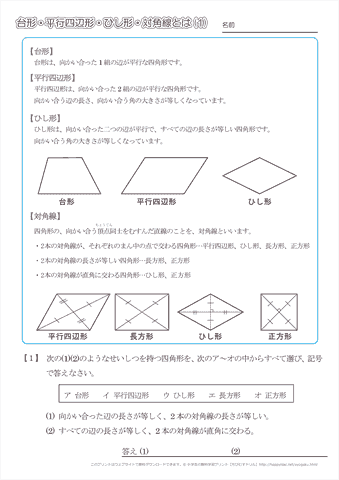 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 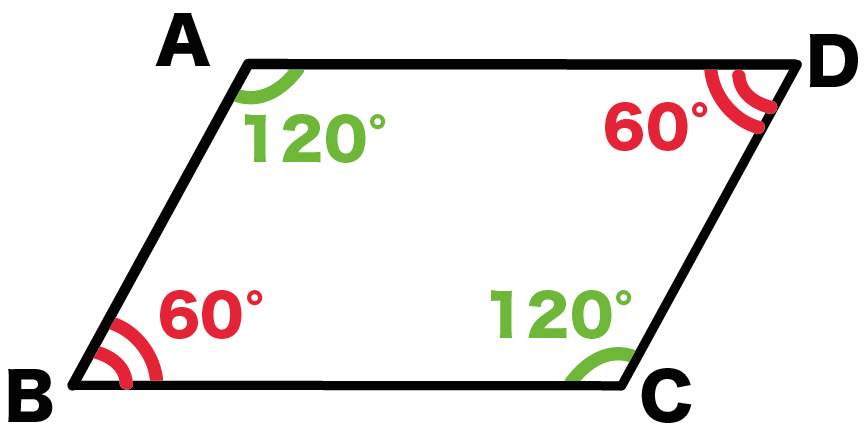 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 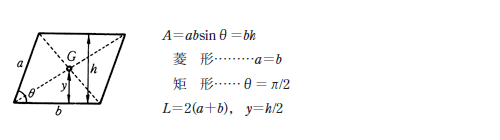 平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 |
平行四辺形の面積の公式 算数の公式 | 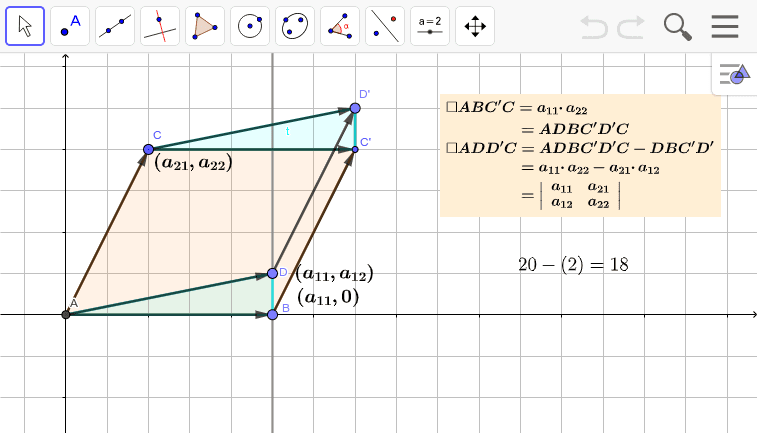 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 | 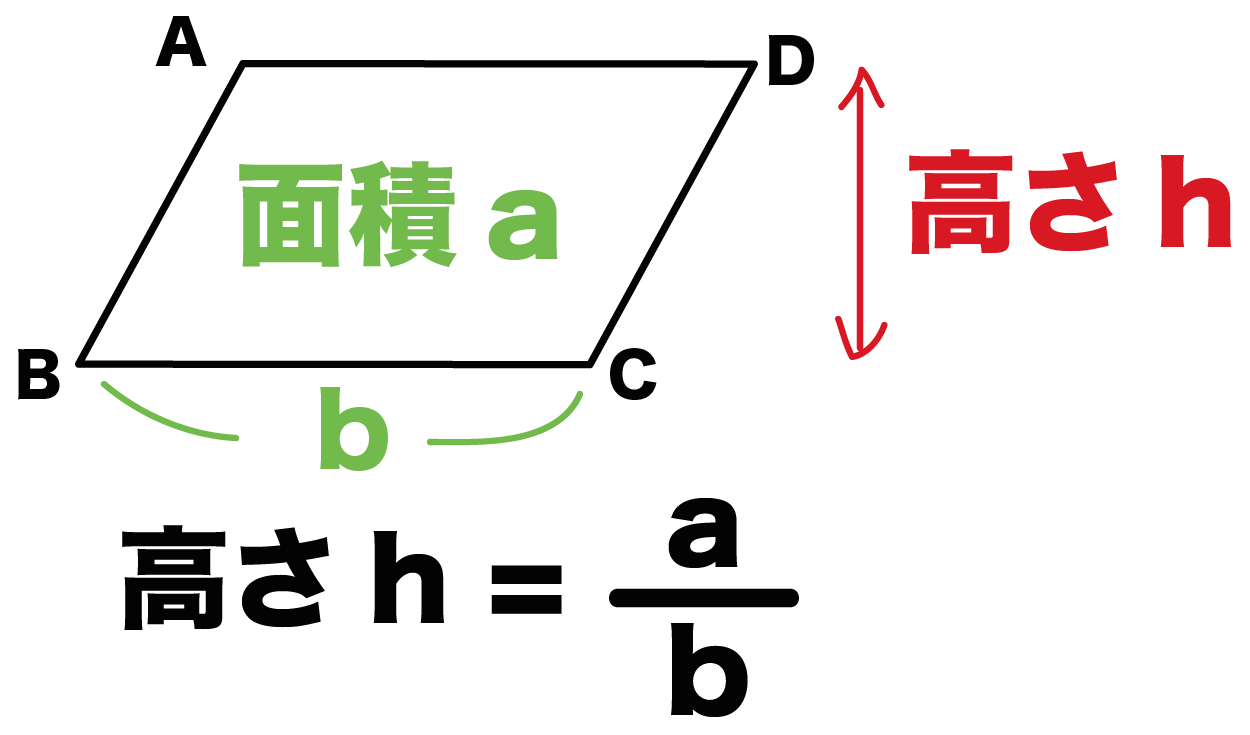 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
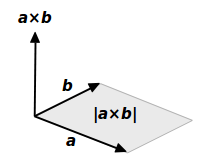 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 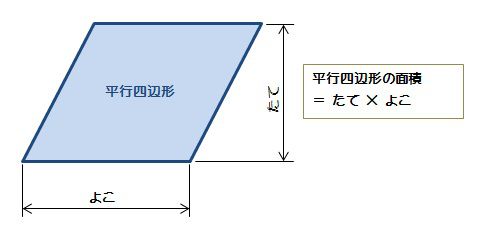 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 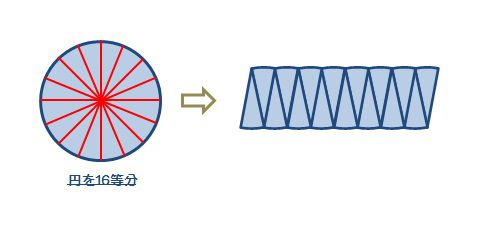 平行四辺形の面積の公式 算数の公式 | 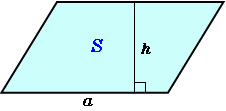 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 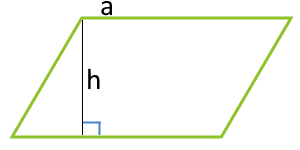 平行四辺形の面積の公式 算数の公式 |
平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 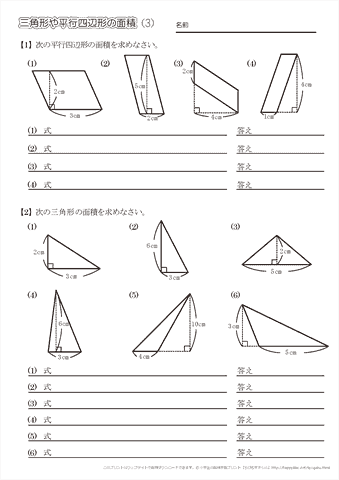 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 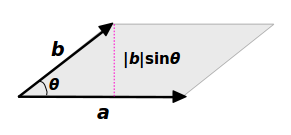 平行四辺形の面積の公式 算数の公式 | 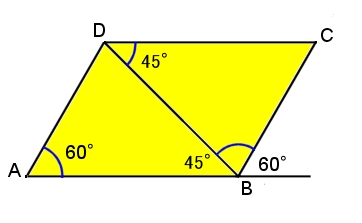 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 |
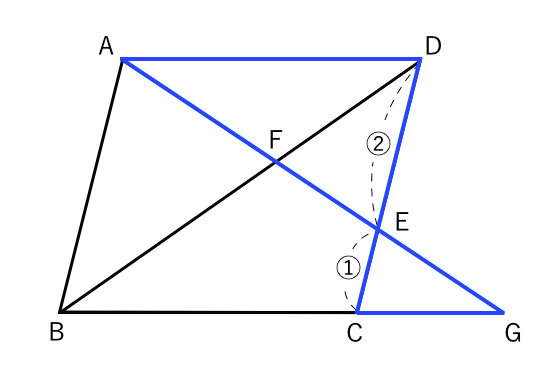 平行四辺形の面積の公式 算数の公式 | 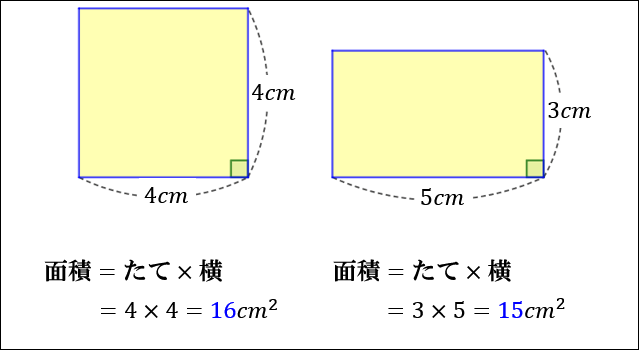 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 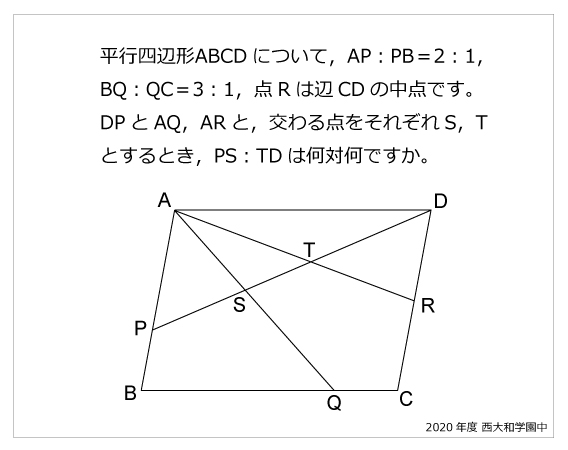 平行四辺形の面積の公式 算数の公式 |
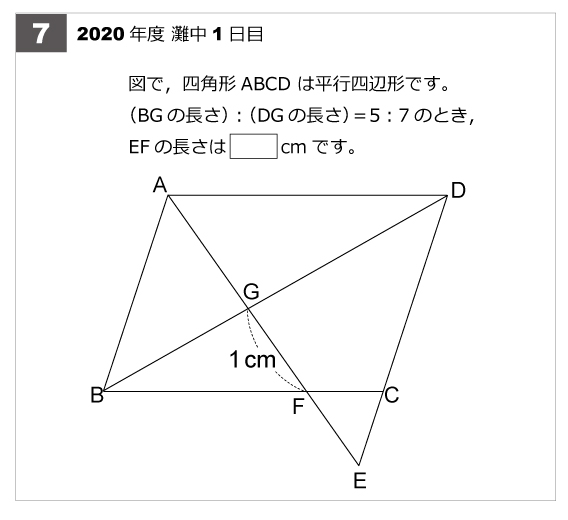 平行四辺形の面積の公式 算数の公式 | 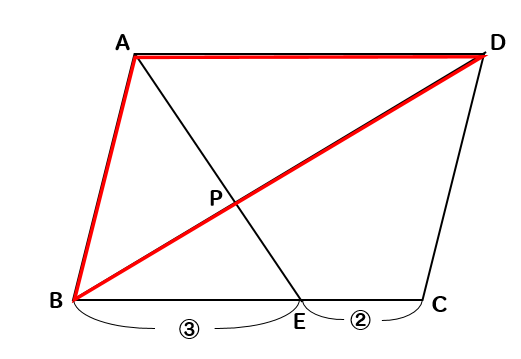 平行四辺形の面積の公式 算数の公式 | 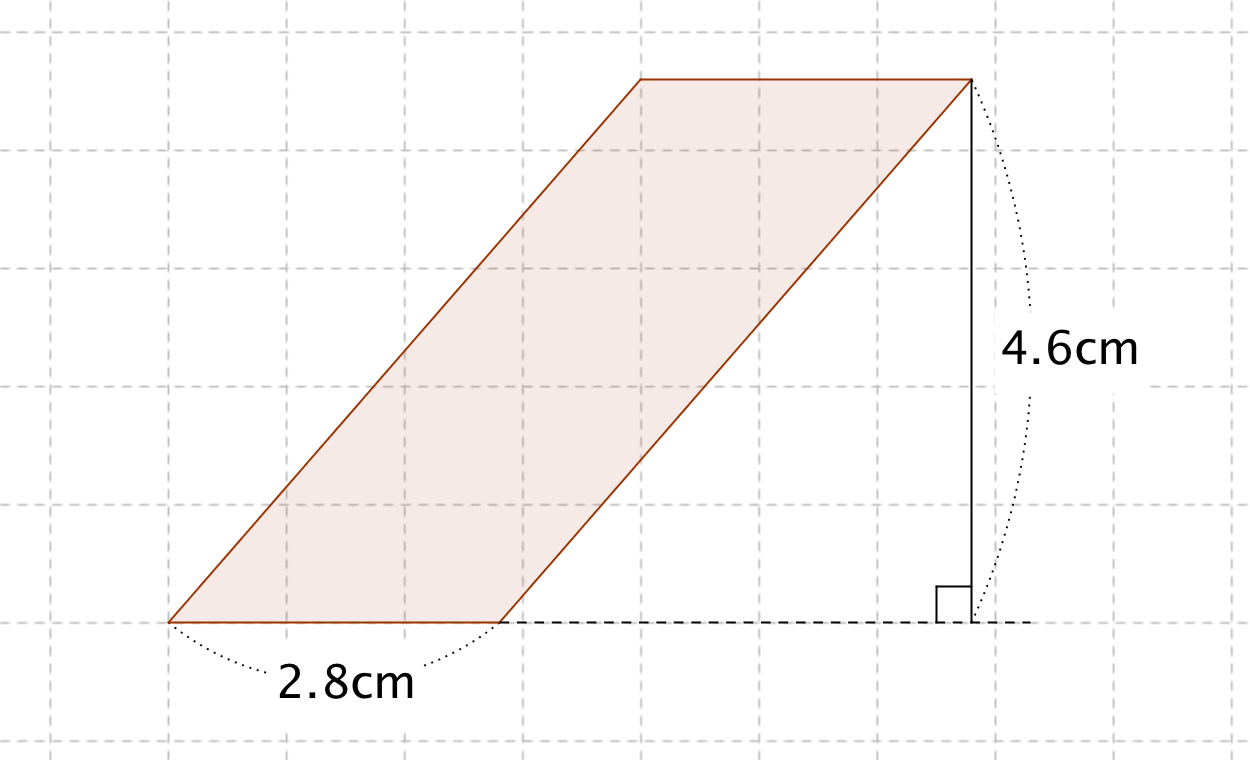 平行四辺形の面積の公式 算数の公式 |
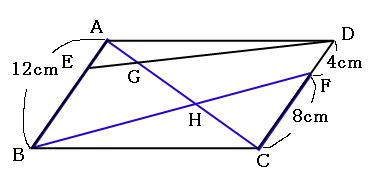 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 | 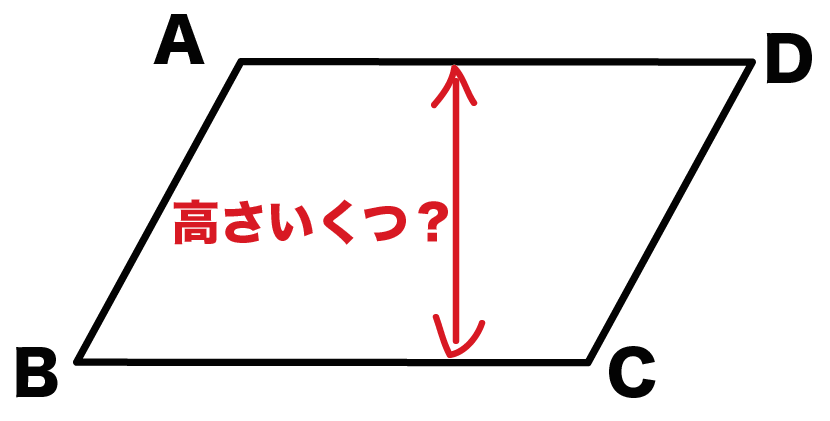 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
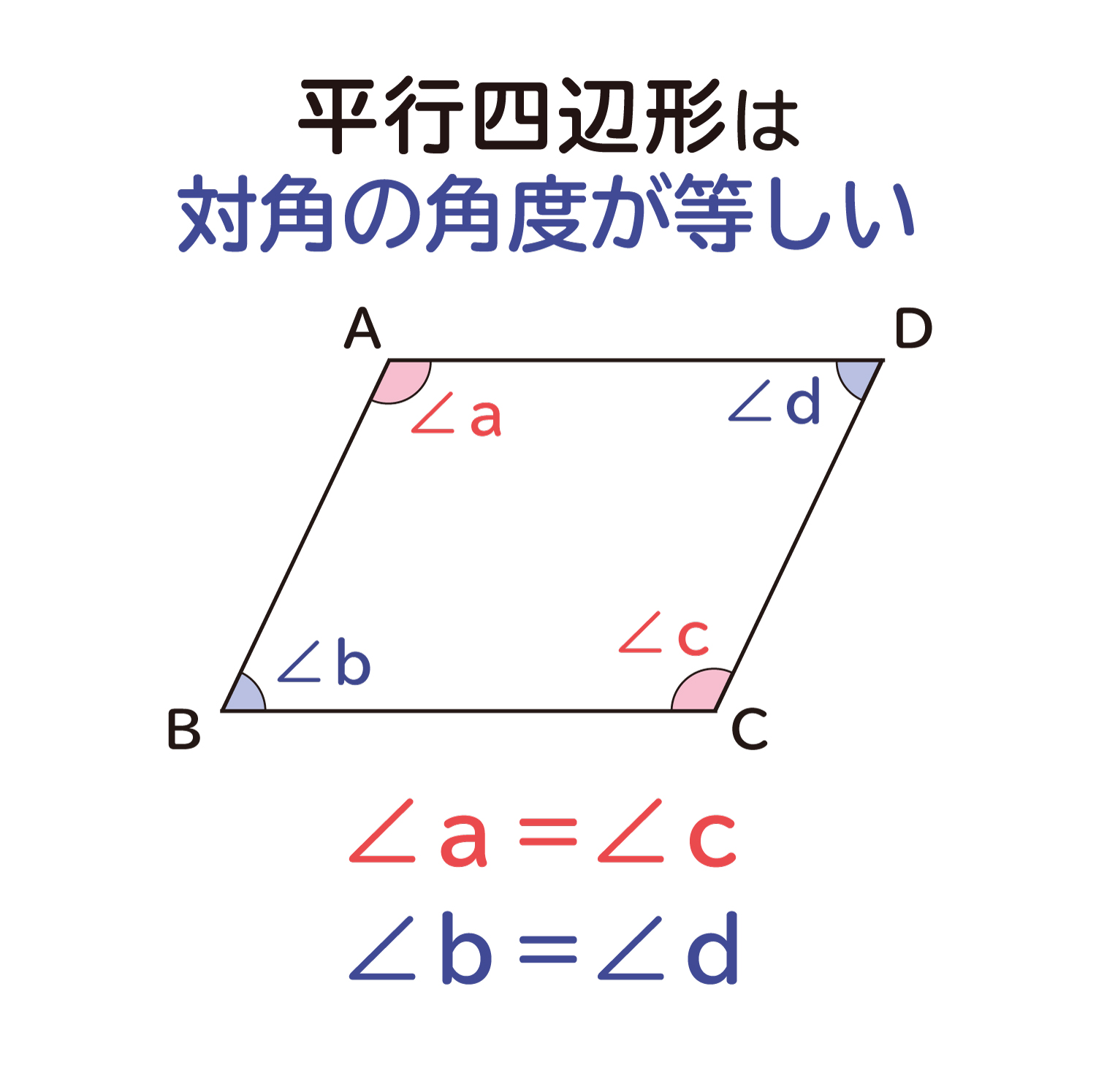 平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 |
平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
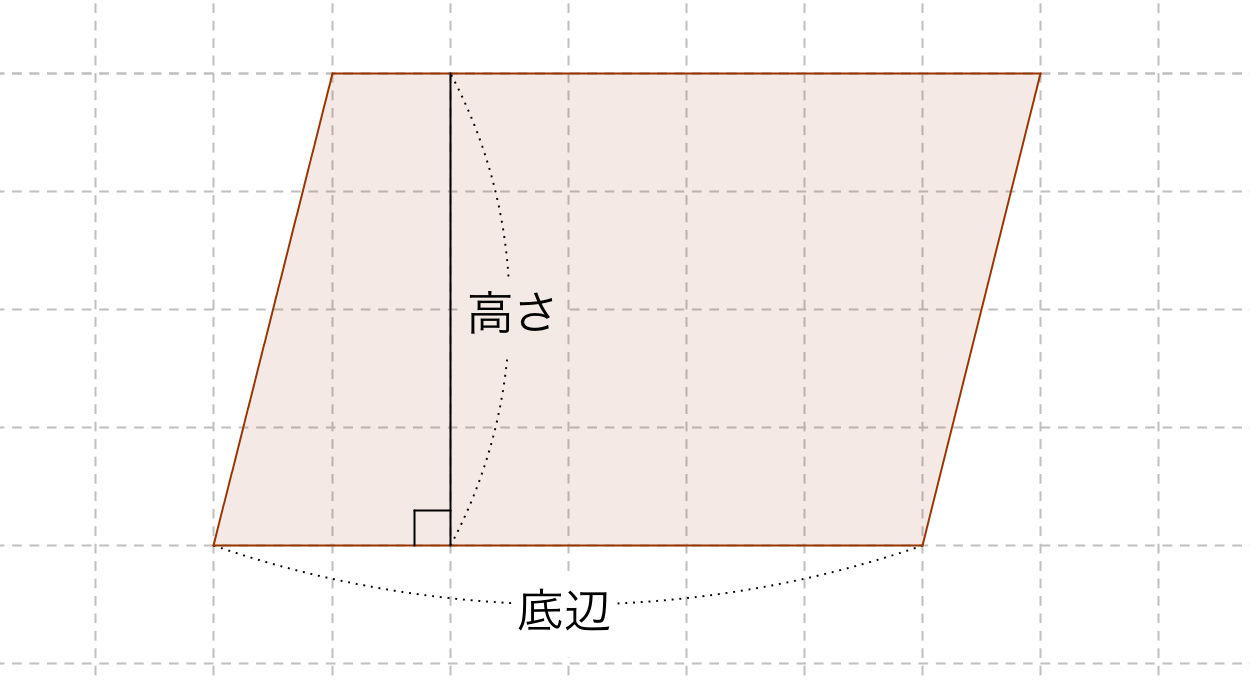 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 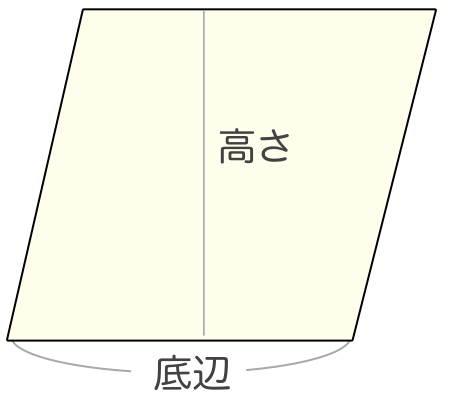 平行四辺形の面積の公式 算数の公式 |  平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 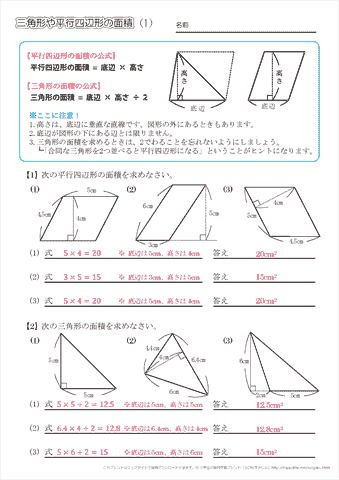 平行四辺形の面積の公式 算数の公式 | 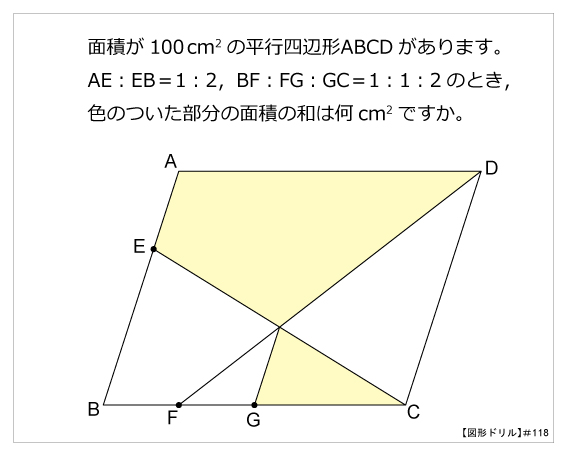 平行四辺形の面積の公式 算数の公式 |
 平行四辺形の面積の公式 算数の公式 | 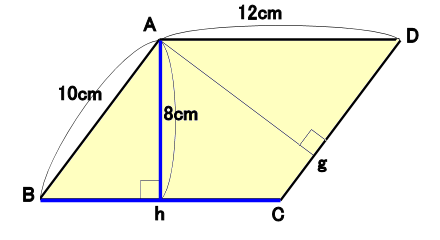 平行四辺形の面積の公式 算数の公式 | 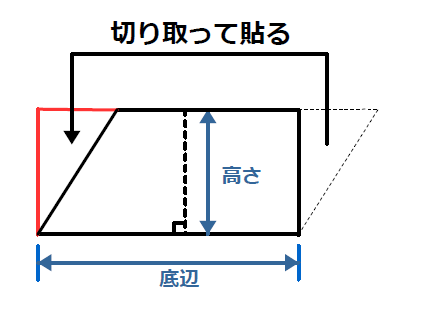 平行四辺形の面積の公式 算数の公式 |
平行四辺形の面積の公式 算数の公式 | 平行四辺形の面積の公式 算数の公式 |
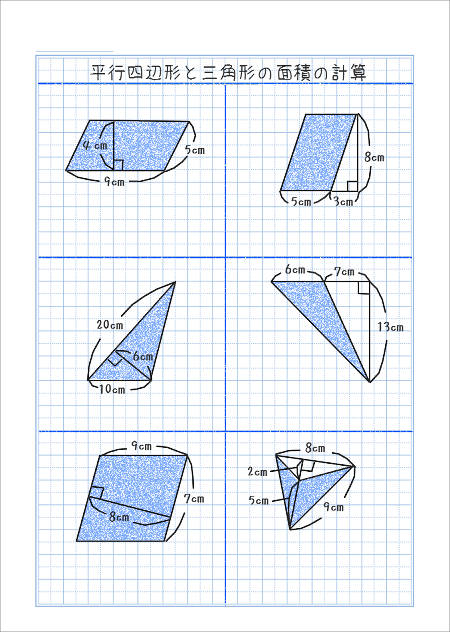
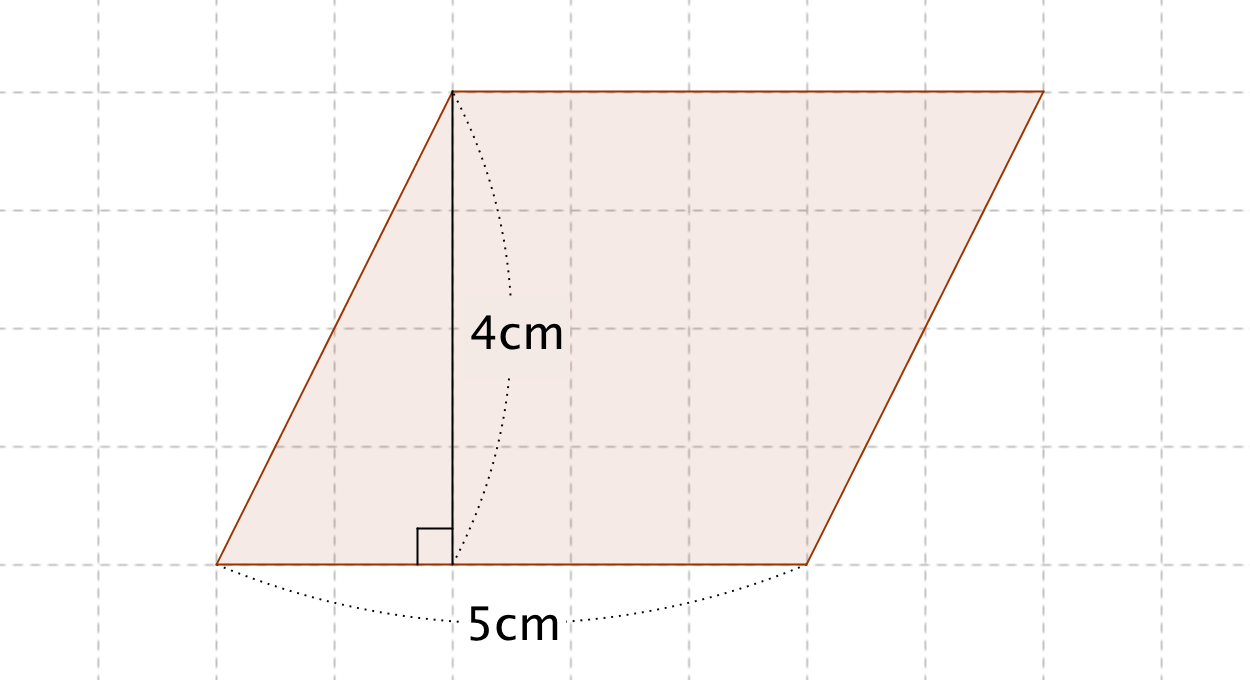
C1:こうして,平行四辺形をつくって求めました。この平行四辺形の面積は,底辺が5㎝で高 さが4㎝なので,面積は になります。三角形の面積は,その半分の10 です。áá T :前と同じように平行四辺形にして考えてくれたね。他にはどうですか?Km 2 /計算 クリア スポン





0 件のコメント:
コメントを投稿